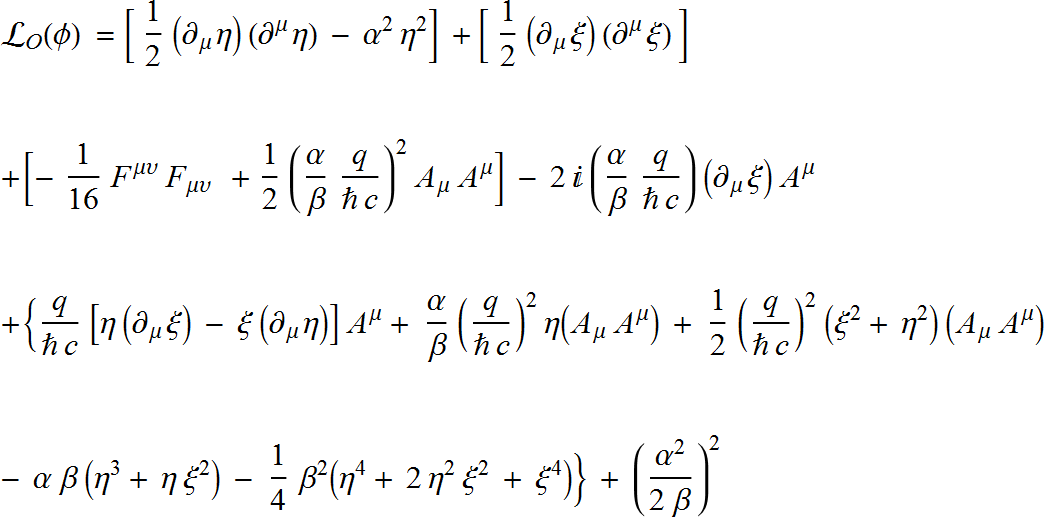In this post I give an detailed description of the process of the Revolution of Matter.
The Hartle-Hawking no-boundary proposal holds that the identity of time and space become indistinguishable as the universal wave function approaches $\mathbb{U}_i$, this requires transforming from $\mathbb{R}^{1,3}$ to $\mathbb{R}^{4}$ as the Klein-Gordon equation reduces in the ground state of the potential well to the non-relativistic Schrödinger's equation, and I have shown this leads to a geometric phase shift,
$$\mid \psi(T) \rangle_\mathbb{U_i} = e^{i[\gamma(t) - \theta(t)]} \quad \mid \psi(T(0)) \rangle $$
where the $\gamma$(t) depends on how the particle evolves through space,
$$\gamma_n(t) = i \int \langle \psi_n \mid \nabla_R \mid
\psi_n
\rangle \cdot dR$$
The vacuum energy does not change from undergoing a geometric phase shift, as from the vacuum expectation value,
$$\langle O \rangle = \langle \psi \mid e^{-i \gamma_n (t)} e^{ \theta(t)} e^{i \gamma_n (t)} e^{ -\theta(t)} \mid \psi \rangle = \langle \psi^* \psi \rangle$$
In the case of the geometric phase shift the antiparticle $\psi_1$ upon reflection into $\psi_2$ does not return to its original point of origin $\mathcal{I}$ for the space has expanded, so
$\psi_2$
now is attempting to move into the state of another particle $\psi_3$ , because the state of the particle is defined by not only its mass, charge, spin, energy but also its place in space and time.
This is an example of the dynamical Casimir Effect within the context of a potential of time varying width.
This is clearly a nonholonomic process, driven by two different phases,
1: The dynamic phase $e^{-\theta(t)}$ of the particles evolving cyclically along $X_i$
2: The geometric phase $e^{\gamma(t)}$ of the potential evolving adiabatically along $X_i$
The two phases are equivalent to two different clocks, the internal clock $T_i$ or the frequency of the virtual particle as it evolves through $\mathbb{R}^{1,3}$, and the external clock $T_e$ for the potential well derived from the adiabatic cycle caused by the intrinsic uncertainty of width R, and allows an exact solution of the universal wave function that includes admixtures of other states,
$$\Psi(x,t) = \psi_n(x,t) e^{i (\gamma (t)-\theta (t))} + \epsilon \sum_{m\neq n} c_m \psi_n(x,t)$$
$$\epsilon =\frac{T_{\text{internal}}}{T_{\text{external}}}$$
"Where $\epsilon$ characterizes the departure from adiabaticity (it goes to zero in the adiabatic limit)" - Griffiths Introduction to Quantum Mechanics
In contradistinction to symmetric and antisymmetric states these extra terms -which I label as asymmetric wave functions- are intrinsically Off Mass-Shell. This is fairly easy to show by taking standing waves in a potential well and adjusting the boundaries non-adiabatically, L $\to$ L + $\delta$L, the original standing waves are now the asymmetric non-solutions in the adjusted well, these asymmetric terms violate conservation of energy and are therefore non-physical. This is a important realization, for it divides the universal wave function into two parts, the first part constitutes the real On Mass-Shell universe and the second the virtual Off Mass-Shell universe of the quantum vacuum. It can been seen real particles lie on the axis of the wave function matrix and virtual particles off the axis, hence I will also refer to this division as on-axis and off-axis particles.
To show the exact formula of the universal wave equation includes the off axis or virtual terms for the quantum vacuum,
$$\Psi(x,t) = \psi_n(x,t) e^{(i \gamma (t)-\theta (t))} + \epsilon \sum_{m\neq n} c_m \psi_n(x,t)$$
start from a static universal wave function,
$$\Psi(x,t) = \Psi_0 e^{
i
( \gamma (t)-\theta (t))} = \Psi_0 e^{i 0} \to \Psi =\Psi_0 : \forall (x,t)=0$$
$$\Psi =
\sum_{m\neq n}
c_{m n} \psi_{m n}=0$$
give this the adiabatic parameter $\epsilon$,
$$\Psi =
\epsilon
\sum_{m\neq n}
c_{m n} \psi_{m n}=0$$
This infinite sea of oscillators is identical to a quantum field, and matches the idea the universe is like a bubble of Hamiltonian action that fluctuates back and forth in time and space, where $\epsilon$ is the variable that shapes and changes the global structure. I can show this by assuming the internal energy of the universe equals the external energy then internal time and external time are in the same proportion as internal action $S_i$ and external action $S_e$,
$$\epsilon =\frac{T_i}{T_e}=\frac{T_i
E_i
}{T_e E_e }=\frac{S_i}{S_e}$$
Since the internal action is comprised of a set of oscillators $\psi$, I can take n as the number of $\psi$ and write $\sigma$ for the action of an internal particle,
$$\epsilon =\frac{n \sigma }{S_e}$$
drop n and consider the action for an arbitrary volume with arbitrary external action S,
$$\epsilon \geq \frac{\sigma }{S}$$
introduce the uncertainties,
$$\epsilon \geq \frac{\sigma }{\text{$\delta $E} \text{$\delta $t}}\geq \frac{\sigma }{E t}\geq \frac{\sigma }{S}$$
$\epsilon$ is a pure number so absorb
$\epsilon$
into $\sigma$ and write it as $\hbar$, the 2$\pi$ comes from the cyclic evolution of the volume,
$$1\geq \frac{\hbar }{\text{$\delta $E} \text{$\delta $t}}\geq \frac{\hbar }{E t}\geq \frac{\hbar }{S}$$
since the volume is arbitrary I can contract this to the size of an elementary particle and derive the energy-time Heisenberg Uncertainty principle,
$$\text{$\delta $t}\geq \frac{\hbar }{\text{$\delta $E}}$$
similarly the exact same technique leads to the momentum-space Heisenberg Uncertainty principle,
$$\text{$\delta $x}\geq \frac{\hbar }{\text{$\delta $p}}$$
So in this model the Heisenberg Uncertainty principle and the adiabatic parameter are directly related, and the evolution of internal particles is directly related to the evolution of the universe as a whole, which on the surface appears similar to Dirac's Large Number Hypothesis (LNH), however, the LNH requires a varying gravitational constant which violates the Perfect Cosmological principle, so for the moment I'm ignoring this possibility. The important part is that the individual dynamics of the internal particles which is governed by the dynamic and geometric phases are derived from the global adiabatic parameter.
Returning to the universal wave equation under the adiabatic parameter and expanding $\Psi$,
$$\Psi =\epsilon \begin{pmatrix}
c_{11} \psi _{11} & c_{12} \psi _{12} & \cdot & c_{1 m} \psi _{1 m}\\
c_{21} \psi _{21} & c_{22} \psi _{22} & \cdot & c_{2 m} \psi _{2 m}\\
\cdot
&
\cdot
& \cdot &
\cdot
\\
c_{n1} \psi _{n1} & c_{n2} \psi _{n2} & \cdot & c_{n m} \psi _{n m}\\ \end{pmatrix}$$
Separate the wave functions of the matrix into on-axis (real matter) and off-axis (virtual particles),
$$\Psi =\epsilon \begin{pmatrix}
c_{11} \psi _{11} & 0 & \cdot & 0\\
0 & c_{22} \psi _{22} & \cdot & 0\\
\cdot
&
\cdot
& \cdot &
\cdot
\\
0 & 0 & \cdot & c_{n m} \psi _{n m}\\ \end{pmatrix} +
\epsilon \begin{pmatrix}
0 & c_{12} \psi _{12} & \cdot & c_{1 m} \psi _{1 m}\\
c_{21} \psi _{21} & 0 & \cdot & c_{2 m} \psi _{2 m}\\
\cdot
&
\cdot
& 0 &
\cdot
\\
c_{n1} \psi _{n1} & c_{n2} \psi _{n2} &
\cdot
& 0\\ \end{pmatrix}
$$
or more conveniently,
$$\Psi =
\epsilon
\sum_{m = n}
c_n \psi_n= \epsilon
\sum_{m\neq n}
c_m \psi_m $$
Make the substitution $\epsilon = e^{i(\gamma-\theta)}$ where the phases arise from fluctuations in the universal potential as equivalent to fluctuations in $\epsilon$, and I can justify this from by the derivation of the Heisenberg Uncertainty principle from the adiabatic parameter, I will also demonstrate exactly how this is possible in another post.
Group the real wave-functions together and sum over the on-axis terms,
$$\Psi = e^{i(\gamma-\theta)} \psi_n + \epsilon
\sum_{m\neq n}
c_m \psi_m $$
Calculate the expectation for $\Psi$,
$$\langle \Psi \mid \Psi \rangle = ( e^{i(\gamma-\theta)} \psi_n + \epsilon
\sum_{m\neq n}
c_m \psi_m
)^* ( e^{i(\gamma-\theta)} \psi_n + \epsilon
\sum_{m\neq n}
c_m \psi_m
)$$
$$ = (e^{-i(\gamma-\theta)} \psi_n + \epsilon
\sum_{m\neq n}
c_m \psi^*_ {m})(e^{i(\gamma-\theta)} \psi_n + \epsilon
\sum_{m\neq n}
c_m \psi_m)$$
expanding,
By definition the m terms are orthogonal to the n terms, so the inner product of $\psi_n$ and $\psi_m$ is zero, reducing $\langle \Psi \mid \Psi \rangle$,
$$
\langle \Psi \mid \Psi \rangle
= (
\psi_n
e^{-i(\gamma-\theta)}
\psi_n
e^{i(\gamma-\theta)} )
+
( \epsilon
\sum_{m\neq n}
c_m \psi^*_ {m} \epsilon
\sum_{m\neq n}
c_m \psi_m)$$
$$
\langle \Psi \mid \Psi \rangle
=
\mid
\psi_n
\mid
^2 +
\quad \epsilon^2
\mid
\sum_{m\neq n}
c_m \psi_{m}
\mid
^2$$
In the adiabatic limit the second term vanishes leaving only On-Mass and On-Axis matter, it is not that the quantum vacuum does not exist but rather its asymmetric expectation is trivial, the on-axis terms are by definition on mass-shell. Remembering "Where
$\epsilon$
characterizes the departure from adiabaticity (it goes to zero in the adiabatic limit)"
- Griffiths Introduction to Quantum Mechanics,
and this is the critical idea, the adiabatic parameter
regularizes
the scalar field and places special constraints on how the Scalar Field can behave, and this now leads to the mechanism by which virtual particles are transformed into matter - which I will address in another post.
testhtmljavascript
Monday, July 28, 2014
Thursday, July 24, 2014
Monopole Suppression
It is possible to show Monopole Suppression takes place at the Big Bang as follows, in discussing the Aharonov-Bohm effect Berry showed for $\mathbb{R}^3$ that $\mathbb{B}$ can be written as the magnetic flux,
$$\Phi _B = \oint_\Sigma \mathbb{B}\cdot d\Sigma = \oint_\Sigma (\nabla \times \mathbb{A}) \cdot d\Sigma$$
where $\mathbb{A}$ is written in terms of the Berry connection,
$$\mathbb{A} = i \langle \psi_n \mid \nabla _R \mid \psi_n \rangle$$
and noting the relation to Berry's geometric phase,
$$\gamma (t) = i \int \langle \psi_n \mid \nabla_R \mid \psi_n \rangle \cdot d\mathbb{R}$$
Given $ \mathbb{B} = \nabla \times \mathbb{A}$
$$\mathbb{B} = i \nabla_R \times \langle \psi_n \mid \nabla_R \mid \psi_n \rangle$$
and Gauss's Theorem,
$$\Phi _B = \oint_\Sigma \mathbb{B}\cdot d\Sigma = \int \int \int_V (\nabla \cdot \mathbb{B} ) dV$$
By the gHH the volume in $\mathbb{R}^3$ is arbitrarily small, so the divergence theorem applies, and passing the imaginary i over the Del,
$$\nabla_R \cdot \mathbb{B} = i \nabla_R \cdot \nabla_R \times \langle \psi_n \mid \nabla_R \mid \psi_n \rangle$$
since the vector identity of the triple vector product of $\mathbb{A}$,
$$\nabla \cdot \nabla \times \mathbb{A} = 0$$
reduces the divergence of $\mathbb{B}$ to,
$$\nabla_R \cdot \mathbb{B} = i \nabla_R \cdot \nabla_R \quad \times \langle \psi_n \mid \nabla_R \mid \psi_n \rangle = 0$$
so the magnetic flux,
This proves that no isolated magnetic flux could exist in the context of the inflationary period of the Big Bang and since an isolated magnetic flux is the definition of a magnetic monopole:
$$\Phi _B = \oint_\Sigma \mathbb{B}\cdot d\Sigma = \oint_\Sigma (\nabla \times \mathbb{A}) \cdot d\Sigma$$
where $\mathbb{A}$ is written in terms of the Berry connection,
$$\mathbb{A} = i \langle \psi_n \mid \nabla _R \mid \psi_n \rangle$$
and noting the relation to Berry's geometric phase,
$$\gamma (t) = i \int \langle \psi_n \mid \nabla_R \mid \psi_n \rangle \cdot d\mathbb{R}$$
Given $ \mathbb{B} = \nabla \times \mathbb{A}$
$$\mathbb{B} = i \nabla_R \times \langle \psi_n \mid \nabla_R \mid \psi_n \rangle$$
and Gauss's Theorem,
$$\Phi _B = \oint_\Sigma \mathbb{B}\cdot d\Sigma = \int \int \int_V (\nabla \cdot \mathbb{B} ) dV$$
By the gHH the volume in $\mathbb{R}^3$ is arbitrarily small, so the divergence theorem applies, and passing the imaginary i over the Del,
$$\nabla_R \cdot \mathbb{B} = i \nabla_R \cdot \nabla_R \times \langle \psi_n \mid \nabla_R \mid \psi_n \rangle$$
since the vector identity of the triple vector product of $\mathbb{A}$,
$$\nabla \cdot \nabla \times \mathbb{A} = 0$$
reduces the divergence of $\mathbb{B}$ to,
$$\nabla_R \cdot \mathbb{B} = i \nabla_R \cdot \nabla_R \quad \times \langle \psi_n \mid \nabla_R \mid \psi_n \rangle = 0$$
so the magnetic flux,
This proves that no isolated magnetic flux could exist in the context of the inflationary period of the Big Bang and since an isolated magnetic flux is the definition of a magnetic monopole:
Therefore the principle of Revolution of Matter predicts that no magnetic monopoles could evolve during the Big Bang.
Monday, July 21, 2014
A Derivation of the Higgs Mechanism from the Geometric Potential
Excerpts from
The Revolution of Matter
This derivation of the Higgs Mechanism follows closely D.Griffiths exposition of the Higgs Mechanism from Introduction to Elementary Particles publisher John Wiley & Sons 1987.
note: if your browser is having trouble rendering the Latex try viewing this blog in Chrome.
Since Euclidean space is non-physical and purely mathematical, I expect the Euclidean Hamiltonian to describe a massless, chargeless and spinless particle, essentially a geometric wave, so let $\mathcal{H}_E (\phi)$ be a function of a massless, chargeless and spinless scalar field $\phi$ in $\mathbb{R}^4$
$$\mathcal{H}_E (\phi) =\mathbb{T} (\phi) -\mathbb{U} (\phi) =0$$
As time tends to the beginning of the universe $\mathbb{U}_i$, the universe takes the form of an infinite square potential, the ground state of which can be approximated by an inverted even quadratic Gaussian function, write $\mathcal{H}_O(\phi)$ for the ground state Euclidean Hamiltonian and call this the New Hamiltonian where $\alpha$ is an arbitrary constant,
$$\mathbb{U} (\phi) =-e^{-(\alpha \phi )^2}$$
Expanding $ \mathbb{U} (\phi) $ under a Taylor series,
$$\mathbb{U} (\phi) \simeq -1 +\alpha ^2 \phi ^2 -\frac{\alpha ^4 \phi ^4}{2} + \frac{\alpha ^6 \phi ^6}{6}-O[ \phi ]$$
ignoring the constant and higher terms leads to,
$$\mathbb{U} (\phi) \simeq \alpha ^2 \phi ^2 -\frac{\alpha ^4 \phi ^4}{2}$$
For low values of $\alpha$ and $\phi$ then $ \mathbb{U} (\phi) $ has the profile of the bottom a wine bottle.
So the New Hamiltonian becomes,
$$ \mathcal{H}_O( \phi )={\partial _\mu }\partial ^{\mu }\phi - \alpha^2 \phi ^2+\frac{\alpha ^4 \phi ^4}{2}=0$$
Rewriting the new Lagrangian and note in transforming from the Hamiltonian to the Lagrangian the potential terms are inverted again, the New Lagrangian is written $\mathcal{L}_O(\phi)$,
$$ \mathcal{L}_O(\phi) ={\partial _\mu } \phi \partial ^{\mu }\phi - \alpha^2 \phi ^2 +\frac{\alpha ^4 \phi ^4}{2}$$
let, $\beta =\alpha ^2$ and divide by two across the equation,
$$ \mathcal{L}_O(\phi) = \frac {{\partial _\mu } \phi \partial ^{\mu }\phi} {2} - \frac {\alpha^2 \phi ^2} {2} +\frac{\beta ^4 \phi ^4}{4}$$
Even though the energy in $\mathbb{R} ^{1,3} $ is real it can be expressed in the form of a complex field $\phi$,
$$\phi =\phi _1+i \phi _2\in \mathbb{C}$$
$$\mathbb{U} (\phi) =f \left(\phi \phi ^*\right)\in \mathbb{R}$$
this New Lagrangian can now be written,
$$ \mathcal{L}_O(\phi) = \frac {({\partial _\mu } \phi) ^ *( \partial ^{\mu }\phi)} {2} + \frac {\alpha^2 (\phi ^ * \phi) } {2} -\frac{\beta ^2 (\phi ^ * \phi) ^2}{4}$$
-$ \mathbb{U} (\phi) $now has the profile of the Goldstone's Mexican hat potential, where graphically the sequence from infinite square potential to sombrero is,
To make the system invariant under local gauge transformations,
$$\phi \to e^{i \theta (x)} \phi $$
introduce a massless gauge field $A^{\mu }$ and replace the derivatives with covariant derivatives,
$$\mathcal{D}_{\mu }= {\partial \mu } + i \frac{q}{c \hbar } A_{\mu }$$
$$ \mathcal{L}_O(\phi) = \frac{1}{2} { [(\partial _{\mu }-i \frac{q}{c \hbar }A_{\mu })\phi ^*] [(\partial _{\mu }+i \frac{q}{c \hbar } A^{\mu } )\phi ] } + \frac {\alpha^2 (\phi ^ * \phi) } {2} -\frac{\beta ^2 (\phi ^ * \phi) ^2}{4} -\frac{1}{16}F^{\mu \upsilon } F_{\mu \upsilon }$$
rewrite the fields as they fluctuate around the ground state,
$$\eta =\phi _1-\frac{\alpha }{\beta } \quad ; \quad \xi =\phi _2$$
expand $ \mathcal{L}_O(\phi)$,
This contains both the Higgs boson and the Goldstone boson, to remove the Goldstone boson use the global invariance of,
$$\phi \to e^{\phi i \theta }\phi$$
$$\phi \to \phi' = (Cos \theta + i Sin \theta)(\phi_1 + i \phi_2) = (\phi_1 Cos \theta - \phi_2 Sin \theta) + i (\phi_1 Sin \theta + \phi_2 Cos \theta)$$
choose,
$$\theta = - tan^{-1} (\frac{\phi_1}{\phi_2})$$
then $\phi'$ is real when $\phi_2$ = 0 then $\xi$ = 0, and the new Lagrangian reduces to,
which is all but identical to the Higgs mechanism barring the $\beta^2 = \alpha$ factor, this leads to,
Importantly the first term is the Klein-Gordon wave equation for a mass $\alpha$, and bearing in mind that as the energy of the system nears zero this can be approximated by minimum excitation of Schrödinger equation which is precisely by the Hartle-Hawking state, and $\mathbb{U}(\phi) $ can now be seen to be the Higgs Potential.
$$\mathbb{U}(\phi) = - e^{(\alpha \phi)^2} \simeq + \alpha^2 \phi^2 - \frac{\alpha^4 \phi^4 }{2}$$
So starting from the premise of Euclidean space transforming into the Minkowski Spacetime under the Wick rotation this introduces a new potential $\mathbb{U}(\phi) $ of a scalar field, upon examining the lowest orders of its expansion and taking into account global invariance of local gauge transformations leads directly to the Higgs boson, the non-physical Goldstone particle exists in $\mathbb{R}^4$ and the physical Higgs boson exists in $\mathbb{R}^{(1,3)}$. Importantly this is a derivation from first principles, Goldstone et al. took this potential as an ansatz - yet for the present model the Lagrangian is imposed by the necessary assumption of a square infinite potential as an inverted even quadratic Gaussian function, so the proof is forced by the necessities of the mathematics to yield a Lagrangian that is all but identical to the Lagrangian for the Higgs mechanism. It can be seen in this model the Higgs particle is derived from the Euclidean space and not Minkowski Spacetime.
Note again, this derivation is largely taken from Griffiths Introduction to Elementary Particles publisher John Wiley & Sons 1987.
In succeeding posts to this blog I'm intending to discuss other features of my paper The Revolution of Matter.
This derivation of the Higgs Mechanism follows closely D.Griffiths exposition of the Higgs Mechanism from Introduction to Elementary Particles publisher John Wiley & Sons 1987.
note: if your browser is having trouble rendering the Latex try viewing this blog in Chrome.
Since Euclidean space is non-physical and purely mathematical, I expect the Euclidean Hamiltonian to describe a massless, chargeless and spinless particle, essentially a geometric wave, so let $\mathcal{H}_E (\phi)$ be a function of a massless, chargeless and spinless scalar field $\phi$ in $\mathbb{R}^4$
$$\mathcal{H}_E (\phi) =\mathbb{T} (\phi) -\mathbb{U} (\phi) =0$$
As time tends to the beginning of the universe $\mathbb{U}_i$, the universe takes the form of an infinite square potential, the ground state of which can be approximated by an inverted even quadratic Gaussian function, write $\mathcal{H}_O(\phi)$ for the ground state Euclidean Hamiltonian and call this the New Hamiltonian where $\alpha$ is an arbitrary constant,
$$\mathbb{U} (\phi) =-e^{-(\alpha \phi )^2}$$
Expanding $ \mathbb{U} (\phi) $ under a Taylor series,
$$\mathbb{U} (\phi) \simeq -1 +\alpha ^2 \phi ^2 -\frac{\alpha ^4 \phi ^4}{2} + \frac{\alpha ^6 \phi ^6}{6}-O[ \phi ]$$
ignoring the constant and higher terms leads to,
$$\mathbb{U} (\phi) \simeq \alpha ^2 \phi ^2 -\frac{\alpha ^4 \phi ^4}{2}$$
For low values of $\alpha$ and $\phi$ then $ \mathbb{U} (\phi) $ has the profile of the bottom a wine bottle.
So the New Hamiltonian becomes,
$$ \mathcal{H}_O( \phi )={\partial _\mu }\partial ^{\mu }\phi - \alpha^2 \phi ^2+\frac{\alpha ^4 \phi ^4}{2}=0$$
Rewriting the new Lagrangian and note in transforming from the Hamiltonian to the Lagrangian the potential terms are inverted again, the New Lagrangian is written $\mathcal{L}_O(\phi)$,
$$ \mathcal{L}_O(\phi) ={\partial _\mu } \phi \partial ^{\mu }\phi - \alpha^2 \phi ^2 +\frac{\alpha ^4 \phi ^4}{2}$$
let, $\beta =\alpha ^2$ and divide by two across the equation,
$$ \mathcal{L}_O(\phi) = \frac {{\partial _\mu } \phi \partial ^{\mu }\phi} {2} - \frac {\alpha^2 \phi ^2} {2} +\frac{\beta ^4 \phi ^4}{4}$$
Even though the energy in $\mathbb{R} ^{1,3} $ is real it can be expressed in the form of a complex field $\phi$,
$$\phi =\phi _1+i \phi _2\in \mathbb{C}$$
$$\mathbb{U} (\phi) =f \left(\phi \phi ^*\right)\in \mathbb{R}$$
this New Lagrangian can now be written,
$$ \mathcal{L}_O(\phi) = \frac {({\partial _\mu } \phi) ^ *( \partial ^{\mu }\phi)} {2} + \frac {\alpha^2 (\phi ^ * \phi) } {2} -\frac{\beta ^2 (\phi ^ * \phi) ^2}{4}$$
-$ \mathbb{U} (\phi) $now has the profile of the Goldstone's Mexican hat potential, where graphically the sequence from infinite square potential to sombrero is,
To make the system invariant under local gauge transformations,
$$\phi \to e^{i \theta (x)} \phi $$
introduce a massless gauge field $A^{\mu }$ and replace the derivatives with covariant derivatives,
$$\mathcal{D}_{\mu }= {\partial \mu } + i \frac{q}{c \hbar } A_{\mu }$$
$$ \mathcal{L}_O(\phi) = \frac{1}{2} { [(\partial _{\mu }-i \frac{q}{c \hbar }A_{\mu })\phi ^*] [(\partial _{\mu }+i \frac{q}{c \hbar } A^{\mu } )\phi ] } + \frac {\alpha^2 (\phi ^ * \phi) } {2} -\frac{\beta ^2 (\phi ^ * \phi) ^2}{4} -\frac{1}{16}F^{\mu \upsilon } F_{\mu \upsilon }$$
rewrite the fields as they fluctuate around the ground state,
$$\eta =\phi _1-\frac{\alpha }{\beta } \quad ; \quad \xi =\phi _2$$
expand $ \mathcal{L}_O(\phi)$,
This contains both the Higgs boson and the Goldstone boson, to remove the Goldstone boson use the global invariance of,
$$\phi \to e^{\phi i \theta }\phi$$
$$\phi \to \phi' = (Cos \theta + i Sin \theta)(\phi_1 + i \phi_2) = (\phi_1 Cos \theta - \phi_2 Sin \theta) + i (\phi_1 Sin \theta + \phi_2 Cos \theta)$$
choose,
$$\theta = - tan^{-1} (\frac{\phi_1}{\phi_2})$$
then $\phi'$ is real when $\phi_2$ = 0 then $\xi$ = 0, and the new Lagrangian reduces to,
which is all but identical to the Higgs mechanism barring the $\beta^2 = \alpha$ factor, this leads to,
Importantly the first term is the Klein-Gordon wave equation for a mass $\alpha$, and bearing in mind that as the energy of the system nears zero this can be approximated by minimum excitation of Schrödinger equation which is precisely by the Hartle-Hawking state, and $\mathbb{U}(\phi) $ can now be seen to be the Higgs Potential.
$$\mathbb{U}(\phi) = - e^{(\alpha \phi)^2} \simeq + \alpha^2 \phi^2 - \frac{\alpha^4 \phi^4 }{2}$$
So starting from the premise of Euclidean space transforming into the Minkowski Spacetime under the Wick rotation this introduces a new potential $\mathbb{U}(\phi) $ of a scalar field, upon examining the lowest orders of its expansion and taking into account global invariance of local gauge transformations leads directly to the Higgs boson, the non-physical Goldstone particle exists in $\mathbb{R}^4$ and the physical Higgs boson exists in $\mathbb{R}^{(1,3)}$. Importantly this is a derivation from first principles, Goldstone et al. took this potential as an ansatz - yet for the present model the Lagrangian is imposed by the necessary assumption of a square infinite potential as an inverted even quadratic Gaussian function, so the proof is forced by the necessities of the mathematics to yield a Lagrangian that is all but identical to the Lagrangian for the Higgs mechanism. It can be seen in this model the Higgs particle is derived from the Euclidean space and not Minkowski Spacetime.
Note again, this derivation is largely taken from Griffiths Introduction to Elementary Particles publisher John Wiley & Sons 1987.
In succeeding posts to this blog I'm intending to discuss other features of my paper The Revolution of Matter.
Saturday, July 5, 2014
generalizaton of the Hartle-Hawking no boundary proposal and the Perfect Cosmological Principle
Excerpts from
The Revolution of Matter
Writing the Euclidean Hamiltonian as a function of a scalar field and allowing the total energy of Euclidean space to be zero, where the dynamical variables momentum and energy are dimensionless in $\mathbb{R}^4$, and accordingly any wave equation is a purely mathematical object.
$$\mathcal{H}_E (\phi) =\mathbb{T} (\phi) -\mathbb{U} (\phi) =0$$
note: if your browser is having trouble rendering the Latex try viewing this blog in Chrome.
Here $\mathbb{U} (\phi)$ is the geometric potential for the entire universe of $\mathbb {R^4} (\phi) $, and since $\mathbb { R^{1,3}}$ is a subspace of $\mathbb{R}^4$ any global change in $\mathbb{U} (\phi)$ causes a global change in $\mathbb {R^{1,3}}$. Under the premise that no physical matter existed before the Big Bang at $\mathbb{U}_i$, then matter is absent in $\mathbb {R^{1,3}}$ and the dynamical variables T, V are zero,
$$\mathcal{H}_M(\mathbb{R}^{1,3})=T+V -G =0$$
$$T=V=G=0$$
Therefore initially $\mathbb {R^{1,3}}$ is as flat as $\mathbb{R}^4$ . Since $\mathcal{H}_E (\phi)$ = 0, this implies -and most importantly - there is no center or boundaries to $\mathbb{U}$, for as the momentum and energy tends to zero so the Heisenberg uncertainties in position and time also tend to infinity,
And this is the key idea, applying the Heisenberg uncertainties to the Euclidean and Minkowskian spaces as a whole states the total uncertainty in space and time tends to infinity,
$$X_i\simeq X_i\pm \text{$\delta $X}_i\simeq X_i\pm \infty$$
So the boundary to any point is at infinity, which is a restatement of the Hartle-Hawking no boundary proposal. Yet adding the maximal uncertainty to the boundary itself,
$$X_i\simeq X_{\max }\pm \text{$\delta $X}_{\max }$$
implies the boundary simultaneously coincides with every other point within this model universe and has the remarkable result that every point within the potential behaves as a boundary of the potential.
In effect, at $\mathbb{U}_i$ where starting from a homogeneous and isotropic $\mathbb{R}^4$ and then applying the Heisenberg Uncertainty principle to $\mathcal{H}_E$ as $\mathbb{R}^4$ evolves smoothly under the Wick Transformation into $\mathbb {R^{1,3}}$ to the $\mathcal{H}_M$ results in every point in $\mathbb {R^{1,3}}$ being bounded and adjacent to every other point in $\mathbb {R^{1,3}}$ , therefore at the Big Bang every point in $\mathbb {R^{1,3}}$ is homogeneous and isotropically identical to every other point which is of course the Perfect Cosmological Principle.
The maximal uncertainty in the position of the boundary also places each point $x_i$ at infinity, this contradiction is resolved by noting the statistical nature of Heisenberg's Uncertainty principle, it follows that any particles reflecting off the boundary do so with a statistical expectation and therefore the boundary has a probability of position - the boundary is simultaneously at infinity and every point within the potential.
This is a generalization of the Hartle-Hawking no boundary proposal, strictly speaking the uncertainty in the boundary has it everywhere as opposed to placing the boundary at infinity, accordingly I call this the generalized Hartle-Hawking no boundary proposal (gHH).
This has three important ideas
1: A universe with zero total energy which is necessary for evolving a universe out of nothing,
2: each point in spacetime is in contact with every other point, which leads to the Perfect Cosmological Principle,
3: the Hartle-Hawking proposal of the universe where having no beginning which removes the problem of a primal cause for the universe.
In succeeding posts to this blog I'm intending to discuss other features of my paper The Revolution of Matter.
copyright © today
Writing the Euclidean Hamiltonian as a function of a scalar field and allowing the total energy of Euclidean space to be zero, where the dynamical variables momentum and energy are dimensionless in $\mathbb{R}^4$, and accordingly any wave equation is a purely mathematical object.
$$\mathcal{H}_E (\phi) =\mathbb{T} (\phi) -\mathbb{U} (\phi) =0$$
note: if your browser is having trouble rendering the Latex try viewing this blog in Chrome.
Here $\mathbb{U} (\phi)$ is the geometric potential for the entire universe of $\mathbb {R^4} (\phi) $, and since $\mathbb { R^{1,3}}$ is a subspace of $\mathbb{R}^4$ any global change in $\mathbb{U} (\phi)$ causes a global change in $\mathbb {R^{1,3}}$. Under the premise that no physical matter existed before the Big Bang at $\mathbb{U}_i$, then matter is absent in $\mathbb {R^{1,3}}$ and the dynamical variables T, V are zero,
$$\mathcal{H}_M(\mathbb{R}^{1,3})=T+V -G =0$$
$$T=V=G=0$$
Therefore initially $\mathbb {R^{1,3}}$ is as flat as $\mathbb{R}^4$ . Since $\mathcal{H}_E (\phi)$ = 0, this implies -and most importantly - there is no center or boundaries to $\mathbb{U}$, for as the momentum and energy tends to zero so the Heisenberg uncertainties in position and time also tend to infinity,
And this is the key idea, applying the Heisenberg uncertainties to the Euclidean and Minkowskian spaces as a whole states the total uncertainty in space and time tends to infinity,
$$X_i\simeq X_i\pm \text{$\delta $X}_i\simeq X_i\pm \infty$$
So the boundary to any point is at infinity, which is a restatement of the Hartle-Hawking no boundary proposal. Yet adding the maximal uncertainty to the boundary itself,
$$X_i\simeq X_{\max }\pm \text{$\delta $X}_{\max }$$
implies the boundary simultaneously coincides with every other point within this model universe and has the remarkable result that every point within the potential behaves as a boundary of the potential.
In effect, at $\mathbb{U}_i$ where starting from a homogeneous and isotropic $\mathbb{R}^4$ and then applying the Heisenberg Uncertainty principle to $\mathcal{H}_E$ as $\mathbb{R}^4$ evolves smoothly under the Wick Transformation into $\mathbb {R^{1,3}}$ to the $\mathcal{H}_M$ results in every point in $\mathbb {R^{1,3}}$ being bounded and adjacent to every other point in $\mathbb {R^{1,3}}$ , therefore at the Big Bang every point in $\mathbb {R^{1,3}}$ is homogeneous and isotropically identical to every other point which is of course the Perfect Cosmological Principle.
The maximal uncertainty in the position of the boundary also places each point $x_i$ at infinity, this contradiction is resolved by noting the statistical nature of Heisenberg's Uncertainty principle, it follows that any particles reflecting off the boundary do so with a statistical expectation and therefore the boundary has a probability of position - the boundary is simultaneously at infinity and every point within the potential.
This is a generalization of the Hartle-Hawking no boundary proposal, strictly speaking the uncertainty in the boundary has it everywhere as opposed to placing the boundary at infinity, accordingly I call this the generalized Hartle-Hawking no boundary proposal (gHH).
Hartle-Hawking proposal $X_i\to \infty$
generalized Hartle-Hawking proposal $X_i \to (0,\infty)$
This has three important ideas
1: A universe with zero total energy which is necessary for evolving a universe out of nothing,
2: each point in spacetime is in contact with every other point, which leads to the Perfect Cosmological Principle,
3: the Hartle-Hawking proposal of the universe where having no beginning which removes the problem of a primal cause for the universe.
In succeeding posts to this blog I'm intending to discuss other features of my paper The Revolution of Matter.
copyright © today
Friday, July 4, 2014
A Derivation of Berry's Geometric Phase from the Geometric Potential
Excerpts from
The Revolution of Matter
Following on from the previous derivation of the Higgs Mechanism from the Geometric Potential I'm going to show Berry's Geometric Phase is also derivable from the Geometric Potential.
Assume a global phase $\gamma$ for the Geometric Potential
$$\phi \to e^{i \gamma} \phi$$
Take the new Lagrangian for Euclidean space,
$$\mathcal{L}_O = \mathbb{T} (\phi) + \mathbb{U} (\phi) $$
this results in a new action $S_O$ for $\mathbb{R}^4$,
$$S_O = \int \mathcal{L}_O dt = \int \mathbb{T} (\phi) + \mathbb{U} (\phi) dt$$
for the ground state of $\mathbb{U} (\phi)$ the kinetic term $ \mathbb{T} (\phi) $ tends to zero, allowing the geometric phase to be determined in terms of $\mathbb{U} (\phi)$,
$$e^{i \gamma (t)} = e^{i \int \mathbb{U} (\phi)dt } $$
Taking time t as an independent variable, this phase successively becomes,
$$ \int \mathbb{U} dt = - \int - \mathbb{U} dt = - \int (- \frac{\partial \mathbb{U}}{\partial x}) dt dx$$
By Ehrenfest's Theorem and taking $\mathbb{P}$ as the geometric equivalent of momentum in the same way as $\mathbb{T}$ is the geometric equivalent of kinetic energy, (and this is the clever bit),
$$\frac{d \langle \mathbb{P}\rangle }{{dt}} = \langle - \frac{\partial \mathbb{U}}{\partial x} \rangle $$
$$ - \int (- \frac{\partial \mathbb{U}}{\partial x}) dt dx = - \int \frac{d \langle \mathbb{P}\rangle }{{dt}} = - \int \langle \mathbb{P}\rangle \cdot dx$$
Substitute the momentum operator for the n'th level of the infinite square potential in the vicinity of $\mathbb{U}_i$, even though $\hbar$ is dimensionless in $\mathbb{R}^4$ it is included for completeness,
$$ \int \mathbb{U} dt = - \int \langle \mathbb{P}\rangle \cdot dx = - \frac{\hbar }{i} \int \int \psi_n^* \frac{\partial }{\partial x} \psi_n dx \cdot dx$$
Simplify and use the Dirac notation,
$$ \int \mathbb{U} dt = - i \hbar \int \langle \psi_n \mid \nabla_x \mid \psi_n \rangle \cdot dx$$
to determine the phase $\gamma$ of the integral $\int \mathbb{U}$ dt divide by $\hbar$ and the $\hbar$ drops out, then integrate over all space,
$$ \gamma_n(t) = i \int \langle \psi_n \mid \nabla_R \mid \psi_n \rangle \cdot dR$$
exponentiate,
$$e^{i \gamma_n(t)} = e^{ i i \int \langle \psi_n \mid \nabla_R \mid \psi_n \rangle \cdot dR}$$
so the phase is real,
$$i \gamma \in \mathcal{R}$$
giving the wavefunction in terms of a geometric phase,
$$\Psi = \int dx \Psi_0 e^{i \gamma}$$
the extra term applies globally to the potential $\mathbb{U}$ as $\Psi$ evolves, this is equivalent to a global geometric phase change $\gamma$,
$$\phi \to e^{i \gamma} \phi$$
Since this is a global phase change I expect it to apply in both $\mathbb{R}^4$ and $\mathbb{R}^{ (1,3) }$, returning to the new Lagrangian $\mathcal{L}_M$ to include the dynamic phase $e^{\int\mathcal{L}dt}$,
$$e^{\int\mathcal{L_M}dt} = e^{\int\mathbb{U} (\phi)dt} \quad e^{\int\mathcal{L}dt} $$
and finally the universal wave function can be written,
$$\Psi = \int \Psi_0 e^{[\gamma (t) - \theta (t)]}$$
It can be seen that integrating the new potential over time is identical to Berry's Geometric Phase factor from his work on the Adiabatic Theorem, where he showed from the geometrical properties of the parameter space the Hamiltonian of a cyclic quantal adiabatic process will acquire an additional phase $\gamma (C)$. This can be generalized by writing for a Hamiltonian $\hat{\mathcal{H}}$ (X(T)) on a parameter space R = (X,Y,Z...), where C is the circuit over R(T) = R(0), and quantal adiabatic limit T $\to$ $\infty$. Since the natural basis of discrete eigenstates under the Schrödinger equation with energies $E_n$(X) is,
$$\hat{\mathcal{H}} (R(t)) \mid n(R) \rangle = E_n(X) \mid n(R) \rangle $$
with dynamic phase,
$$\theta (T) = - \frac{i}{\hbar } \int _0^T dt E_n(R(t)) $$
and geometric phase over a closed cycle C,
$$ \gamma_n(C) = i \oint \langle \psi_n \mid \nabla_R \mid \psi_n \rangle \cdot dR$$
where Minkowski Spacetime is assumed to be a continuously transformable from Euclidean space and noting the geometric phase is a pure number, it is now possible without loss of generality to use the geometric phase as an additional factor of the wave function in $\mathbb{R}^{1,3}$ as it affects all points in $\mathbb{R}^{1,3}$ equally, allowing,
$$ \mid \psi (T) \rangle_{\mathbb{U}_i} = e^{i [\gamma (C) - \theta (t)] } \mid \psi (T(0)) \rangle$$
The idea that the dynamic phase disappears in the Euclidean domain is consistent with the idea the physical universe having a beginning in Time, where transforming from Euclidean space to Minkowski Spacetime under the Wick rotation at $\mathbb{U}_i$ is equivalent to the switching from a geometric system to a dynamic system, which is essentially the idea behind the Hartle-Hawking no boundary proposal, so remarkably the ideas of Hartle-Hawking and Berry can be combined into a single model.
Importantly this transformation is only possible for a cyclic space in its lowest energy level, and this will be of crucial importance in the construction of a Big Bang model to be addressed later in this paper, - very importantly this additional phase factor in $\mathbb{R}^{1,3}$ is homogeneous and isotropic and affects all particles equally and this crucial idea will be returned to in the section on Newton's First Law.
Following on from the previous derivation of the Higgs Mechanism from the Geometric Potential I'm going to show Berry's Geometric Phase is also derivable from the Geometric Potential.
Assume a global phase $\gamma$ for the Geometric Potential
$$\phi \to e^{i \gamma} \phi$$
Take the new Lagrangian for Euclidean space,
$$\mathcal{L}_O = \mathbb{T} (\phi) + \mathbb{U} (\phi) $$
this results in a new action $S_O$ for $\mathbb{R}^4$,
$$S_O = \int \mathcal{L}_O dt = \int \mathbb{T} (\phi) + \mathbb{U} (\phi) dt$$
for the ground state of $\mathbb{U} (\phi)$ the kinetic term $ \mathbb{T} (\phi) $ tends to zero, allowing the geometric phase to be determined in terms of $\mathbb{U} (\phi)$,
$$e^{i \gamma (t)} = e^{i \int \mathbb{U} (\phi)dt } $$
Taking time t as an independent variable, this phase successively becomes,
$$ \int \mathbb{U} dt = - \int - \mathbb{U} dt = - \int (- \frac{\partial \mathbb{U}}{\partial x}) dt dx$$
By Ehrenfest's Theorem and taking $\mathbb{P}$ as the geometric equivalent of momentum in the same way as $\mathbb{T}$ is the geometric equivalent of kinetic energy, (and this is the clever bit),
$$\frac{d \langle \mathbb{P}\rangle }{{dt}} = \langle - \frac{\partial \mathbb{U}}{\partial x} \rangle $$
$$ - \int (- \frac{\partial \mathbb{U}}{\partial x}) dt dx = - \int \frac{d \langle \mathbb{P}\rangle }{{dt}} = - \int \langle \mathbb{P}\rangle \cdot dx$$
Substitute the momentum operator for the n'th level of the infinite square potential in the vicinity of $\mathbb{U}_i$, even though $\hbar$ is dimensionless in $\mathbb{R}^4$ it is included for completeness,
$$ \int \mathbb{U} dt = - \int \langle \mathbb{P}\rangle \cdot dx = - \frac{\hbar }{i} \int \int \psi_n^* \frac{\partial }{\partial x} \psi_n dx \cdot dx$$
Simplify and use the Dirac notation,
$$ \int \mathbb{U} dt = - i \hbar \int \langle \psi_n \mid \nabla_x \mid \psi_n \rangle \cdot dx$$
to determine the phase $\gamma$ of the integral $\int \mathbb{U}$ dt divide by $\hbar$ and the $\hbar$ drops out, then integrate over all space,
$$ \gamma_n(t) = i \int \langle \psi_n \mid \nabla_R \mid \psi_n \rangle \cdot dR$$
exponentiate,
$$e^{i \gamma_n(t)} = e^{ i i \int \langle \psi_n \mid \nabla_R \mid \psi_n \rangle \cdot dR}$$
so the phase is real,
$$i \gamma \in \mathcal{R}$$
giving the wavefunction in terms of a geometric phase,
$$\Psi = \int dx \Psi_0 e^{i \gamma}$$
the extra term applies globally to the potential $\mathbb{U}$ as $\Psi$ evolves, this is equivalent to a global geometric phase change $\gamma$,
$$\phi \to e^{i \gamma} \phi$$
Since this is a global phase change I expect it to apply in both $\mathbb{R}^4$ and $\mathbb{R}^{ (1,3) }$, returning to the new Lagrangian $\mathcal{L}_M$ to include the dynamic phase $e^{\int\mathcal{L}dt}$,
$$e^{\int\mathcal{L_M}dt} = e^{\int\mathbb{U} (\phi)dt} \quad e^{\int\mathcal{L}dt} $$
and finally the universal wave function can be written,
$$\Psi = \int \Psi_0 e^{[\gamma (t) - \theta (t)]}$$
It can be seen that integrating the new potential over time is identical to Berry's Geometric Phase factor from his work on the Adiabatic Theorem, where he showed from the geometrical properties of the parameter space the Hamiltonian of a cyclic quantal adiabatic process will acquire an additional phase $\gamma (C)$. This can be generalized by writing for a Hamiltonian $\hat{\mathcal{H}}$ (X(T)) on a parameter space R = (X,Y,Z...), where C is the circuit over R(T) = R(0), and quantal adiabatic limit T $\to$ $\infty$. Since the natural basis of discrete eigenstates under the Schrödinger equation with energies $E_n$(X) is,
$$\hat{\mathcal{H}} (R(t)) \mid n(R) \rangle = E_n(X) \mid n(R) \rangle $$
with dynamic phase,
$$\theta (T) = - \frac{i}{\hbar } \int _0^T dt E_n(R(t)) $$
and geometric phase over a closed cycle C,
$$ \gamma_n(C) = i \oint \langle \psi_n \mid \nabla_R \mid \psi_n \rangle \cdot dR$$
where Minkowski Spacetime is assumed to be a continuously transformable from Euclidean space and noting the geometric phase is a pure number, it is now possible without loss of generality to use the geometric phase as an additional factor of the wave function in $\mathbb{R}^{1,3}$ as it affects all points in $\mathbb{R}^{1,3}$ equally, allowing,
$$ \mid \psi (T) \rangle_{\mathbb{U}_i} = e^{i [\gamma (C) - \theta (t)] } \mid \psi (T(0)) \rangle$$
The idea that the dynamic phase disappears in the Euclidean domain is consistent with the idea the physical universe having a beginning in Time, where transforming from Euclidean space to Minkowski Spacetime under the Wick rotation at $\mathbb{U}_i$ is equivalent to the switching from a geometric system to a dynamic system, which is essentially the idea behind the Hartle-Hawking no boundary proposal, so remarkably the ideas of Hartle-Hawking and Berry can be combined into a single model.
Importantly this transformation is only possible for a cyclic space in its lowest energy level, and this will be of crucial importance in the construction of a Big Bang model to be addressed later in this paper, - very importantly this additional phase factor in $\mathbb{R}^{1,3}$ is homogeneous and isotropic and affects all particles equally and this crucial idea will be returned to in the section on Newton's First Law.
Tuesday, July 1, 2014
The Euclidean Hamiltonian and the Wick Rotation
Excerpts from
The Revolution of Matter
Under the Wick Rotation the potential in the Lagrangian or the Hamiltonian for a system switches from positive to negative,
$$ V_E( {R}^4 )\geq 0 \quad \quad \underset{\rightleftarrows }{\text{Wick}} \quad \quad - V_M({R}^{1,3})\leq 0$$
for instance the Minkowskian Hamiltonian switches from
$$ \mathcal{H}_M ( \mathbb{R}^{1,3} ) = T+V>0 $$
to
$$ \mathcal{H}_M ( \mathbb{R}^{4} ) = T-V=0 $$
Obviously the total energies do not match.
$$\mathcal{H}_M(\mathbb{R}^{1,3})\geqslant \mathcal{H}_E (\mathbb{R}^4) $$
Similarly in comparing the Euclidean Lagrangian $\mathcal{L}_E$ to the Minkowski Lagrangian $\mathcal{L}_M$ via the Wick rotation,
$$ \mathcal{L}_E( \mathbb{R}^4 )=\mathbb{T}+\mathbb{U}\geq 0$$
$$\mathcal{L}_M\left(\mathbb{R}^{1,3}\right)=T-V=0$$
$\mathcal{L}_E$ is ordered positive semidefinite to $\mathcal{L}_M$
$$| \mathcal {L}_E (\mathbb{R}^4) | \geqslant | \mathcal{L}_M(\mathbb{R}^{1,3})|$$
It can also be seen the Lagrangians do not match, therefore the Hamiltonian Actions derived from the Lagrangians do not match. To match the Hamiltonians of $\mathbb{R}^4$ to $\mathbb{R}^{1,3}$ requires an additional potential be subtracted from $\mathbb{R}^{1,3}$, and the obvious field is gravity G,
$$\mathcal{H}_M(\mathbb{R}^{1,3})=T+V - G =0$$
This introduction of gravity follows on as Hartle-Hawking put it - "Indeed in a certain sense the total energy for a closed universe is always zero - the gravitational energy cancelling the matter energy." So along with the other potentials V for Electro-Weak and Strong which have charges who energies cancel out, the gravitational potential appears as an extra geometric term to maintain the problem Euclidean flatness in Minkowski spacetime. In effect the gravitational field is a gauge potential that is introduced to maintain zero global energy.
copyright © today
Under the Wick Rotation the potential in the Lagrangian or the Hamiltonian for a system switches from positive to negative,
$$ V_E( {R}^4 )\geq 0 \quad \quad \underset{\rightleftarrows }{\text{Wick}} \quad \quad - V_M({R}^{1,3})\leq 0$$
for instance the Minkowskian Hamiltonian switches from
$$ \mathcal{H}_M ( \mathbb{R}^{1,3} ) = T+V>0 $$
to
$$ \mathcal{H}_M ( \mathbb{R}^{4} ) = T-V=0 $$
Obviously the total energies do not match.
$$\mathcal{H}_M(\mathbb{R}^{1,3})\geqslant \mathcal{H}_E (\mathbb{R}^4) $$
Similarly in comparing the Euclidean Lagrangian $\mathcal{L}_E$ to the Minkowski Lagrangian $\mathcal{L}_M$ via the Wick rotation,
$$ \mathcal{L}_E( \mathbb{R}^4 )=\mathbb{T}+\mathbb{U}\geq 0$$
$$\mathcal{L}_M\left(\mathbb{R}^{1,3}\right)=T-V=0$$
$\mathcal{L}_E$ is ordered positive semidefinite to $\mathcal{L}_M$
$$| \mathcal {L}_E (\mathbb{R}^4) | \geqslant | \mathcal{L}_M(\mathbb{R}^{1,3})|$$
It can also be seen the Lagrangians do not match, therefore the Hamiltonian Actions derived from the Lagrangians do not match. To match the Hamiltonians of $\mathbb{R}^4$ to $\mathbb{R}^{1,3}$ requires an additional potential be subtracted from $\mathbb{R}^{1,3}$, and the obvious field is gravity G,
$$\mathcal{H}_M(\mathbb{R}^{1,3})=T+V - G =0$$
This introduction of gravity follows on as Hartle-Hawking put it - "Indeed in a certain sense the total energy for a closed universe is always zero - the gravitational energy cancelling the matter energy." So along with the other potentials V for Electro-Weak and Strong which have charges who energies cancel out, the gravitational potential appears as an extra geometric term to maintain the problem Euclidean flatness in Minkowski spacetime. In effect the gravitational field is a gauge potential that is introduced to maintain zero global energy.
copyright © today
Subscribe to:
Posts (Atom)