Excerpts from
The Revolution of Matter
This derivation of the Higgs Mechanism follows closely D.Griffiths exposition of the Higgs Mechanism from Introduction to Elementary Particles publisher John Wiley & Sons 1987.
note: if your browser is having trouble rendering the Latex try viewing this blog in Chrome.
Since Euclidean space is non-physical and purely mathematical, I expect the Euclidean Hamiltonian to describe a massless, chargeless and spinless particle, essentially a geometric wave, so let $\mathcal{H}_E (\phi)$ be a function of a massless, chargeless and spinless scalar field $\phi$ in $\mathbb{R}^4$
$$\mathcal{H}_E (\phi) =\mathbb{T} (\phi) -\mathbb{U} (\phi) =0$$
As time tends to the beginning of the universe $\mathbb{U}_i$, the universe takes the form of an infinite square potential, the ground state of which can be approximated by an inverted even quadratic Gaussian function, write $\mathcal{H}_O(\phi)$ for the ground state Euclidean Hamiltonian and call this the New Hamiltonian where $\alpha$ is an arbitrary constant,
$$\mathbb{U} (\phi) =-e^{-(\alpha \phi )^2}$$
Expanding $ \mathbb{U} (\phi)
$ under a Taylor series,
$$\mathbb{U} (\phi) \simeq -1 +\alpha ^2 \phi ^2
-\frac{\alpha ^4 \phi ^4}{2}
+ \frac{\alpha ^6 \phi ^6}{6}-O[
\phi
]$$
ignoring the constant and higher terms leads to,
$$\mathbb{U} (\phi) \simeq \alpha ^2 \phi ^2
-\frac{\alpha ^4 \phi ^4}{2}$$
For low values of $\alpha$ and $\phi$ then
$ \mathbb{U} (\phi)
$
has the profile of the bottom a wine bottle.
So the New Hamiltonian becomes,
$$ \mathcal{H}_O( \phi
)={\partial
_\mu
}\partial ^{\mu }\phi - \alpha^2 \phi ^2+\frac{\alpha ^4 \phi ^4}{2}=0$$
Rewriting the new Lagrangian and note in transforming from the Hamiltonian to the Lagrangian the potential terms are inverted again, the New Lagrangian is written $\mathcal{L}_O(\phi)$,
$$
\mathcal{L}_O(\phi)
={\partial
_\mu
} \phi
\partial ^{\mu }\phi - \alpha^2 \phi ^2 +\frac{\alpha ^4 \phi ^4}{2}$$
let, $\beta =\alpha ^2$ and divide by two across the equation,
$$
\mathcal{L}_O(\phi)
=
\frac
{{\partial
_\mu
}
\phi
\partial ^{\mu }\phi}
{2} -
\frac
{\alpha^2 \phi ^2}
{2}
+\frac{\beta ^4 \phi ^4}{4}$$
Even though the energy in
$\mathbb{R} ^{1,3} $
is real it can be expressed in the form of a complex field $\phi$,
$$\phi =\phi _1+i \phi _2\in \mathbb{C}$$
$$\mathbb{U} (\phi) =f \left(\phi \phi ^*\right)\in \mathbb{R}$$
this New Lagrangian can now be written,
$$
\mathcal{L}_O(\phi)
=
\frac
{({\partial
_\mu
}
\phi) ^
*(
\partial ^{\mu }\phi)}
{2} +
\frac
{\alpha^2 (\phi ^
*
\phi) }
{2}
-\frac{\beta ^2
(\phi ^
*
\phi)
^2}{4}$$
-$ \mathbb{U} (\phi)
$now has the profile of the Goldstone's Mexican hat potential, where graphically the sequence from infinite square potential to sombrero is,
To make the system invariant under local gauge transformations,
$$\phi \to e^{i \theta (x)}
\phi
$$
introduce a massless gauge field $A^{\mu }$ and replace the derivatives with covariant derivatives,
$$\mathcal{D}_{\mu }=
{\partial \mu }
+ i \frac{q}{c \hbar } A_{\mu }$$
$$
\mathcal{L}_O(\phi)
=
\frac{1}{2} {
[(\partial _{\mu }-i \frac{q}{c \hbar }A_{\mu })\phi ^*] [(\partial _{\mu }+i \frac{q}{c \hbar }
A^{\mu }
)\phi ]
}
+
\frac
{\alpha^2 (\phi ^
*
\phi) }
{2}
-\frac{\beta ^2
(\phi ^
*
\phi)
^2}{4} -\frac{1}{16}F^{\mu \upsilon } F_{\mu \upsilon }$$
rewrite the fields as they fluctuate around the ground state,
$$\eta =\phi _1-\frac{\alpha }{\beta } \quad ; \quad \xi =\phi _2$$
expand $
\mathcal{L}_O(\phi)$,
This contains both the Higgs boson and the Goldstone boson, to remove the Goldstone boson use the global invariance of,
$$\phi \to e^{\phi i \theta }\phi$$
$$\phi \to \phi' = (Cos \theta + i Sin \theta)(\phi_1 + i \phi_2) = (\phi_1 Cos \theta - \phi_2 Sin \theta) + i (\phi_1 Sin \theta + \phi_2 Cos \theta)$$
choose,
$$\theta = - tan^{-1} (\frac{\phi_1}{\phi_2})$$
then $\phi'$ is real when $\phi_2$ = 0 then $\xi$ = 0, and the new Lagrangian reduces to,
which is all but identical to the Higgs mechanism barring the $\beta^2 = \alpha$ factor, this leads to,
Importantly the first term is the Klein-Gordon wave equation for a mass $\alpha$, and bearing in mind that as the energy of the system nears zero this can be approximated by minimum excitation of Schrödinger equation which is precisely by the Hartle-Hawking state, and $\mathbb{U}(\phi) $ can now be seen to be the Higgs Potential.
$$\mathbb{U}(\phi) = - e^{(\alpha \phi)^2} \simeq + \alpha^2 \phi^2 - \frac{\alpha^4 \phi^4 }{2}$$
So starting from the premise of Euclidean space transforming into the Minkowski Spacetime under the Wick rotation this introduces a new potential $\mathbb{U}(\phi)
$ of a scalar field, upon examining the lowest orders of its expansion and taking into account global invariance of local gauge transformations leads directly to the Higgs boson, the non-physical Goldstone particle exists in $\mathbb{R}^4$ and the physical Higgs boson exists in $\mathbb{R}^{(1,3)}$. Importantly this is a derivation from first principles, Goldstone et al. took this potential as an ansatz - yet for the present model the Lagrangian is imposed by the necessary assumption of a square infinite potential as an inverted even quadratic Gaussian function, so the proof is forced by the necessities of the mathematics to yield a Lagrangian that is all but identical to the Lagrangian for the Higgs mechanism. It can be seen in this model the Higgs particle is derived from the Euclidean space and not Minkowski Spacetime.
Note again, this derivation is largely taken from Griffiths Introduction to Elementary Particles publisher John Wiley & Sons 1987.
In succeeding posts to this blog I'm intending to discuss other features of my paper The Revolution of Matter.

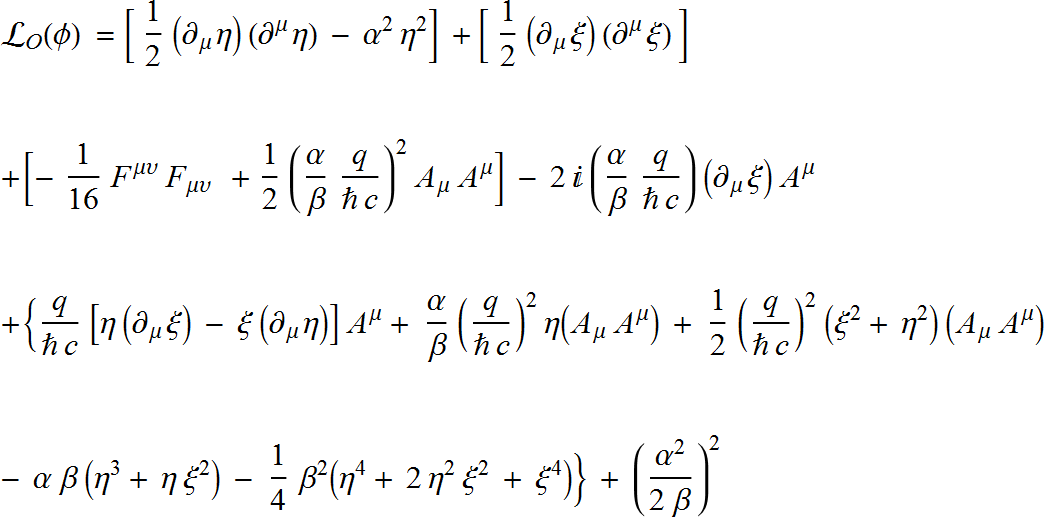


No comments:
Post a Comment